반응형

1. 행렬과 연립방정식
선형대수에서 다루는 연립방정식 시스템은 다음과 같은 형식을 갖습니다:
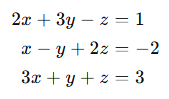
이 방정식을 계수행렬과 확대행렬로 표현할 수 있습니다. 계수 행렬은 각 방정식의 변수에 곱해지는 숫자(계수)들을 모아 놓은 행렬입니다. 간단히 말하여 x,y변수 앞의 수를 계수라 합니다. 위 연립방정식의 계수 행렬은 다음과 같습니다:

여기에 오른쪽 상수 항(값)을 포함한 확대 행렬은 다음과 같습니다.

이 증강 행렬을 변환하여 해를 구하는 것이 가우스 소거법입니다.
2. 가우스 소거법
가우스 소거법은 연립방정식을 풀기 위해 행렬을 단계적으로 변환하는 과정입니다. 주요 목표는 증강 행렬을 상삼각 행렬(Upper Triangular Matrix) 또는 행 기약 사다리꼴(Reduced Row Echelon Form)로 만드는 것입니다.
이를 통해 우리는 미지수 x, y, z에 대한 명확한 답을 구할 수 있습니다. 가우스 소거법의 핵심 과정은 다음 세 가지 행 연산을 통해 이루어집니다. 아래 3가지 방법은 기본행연산으로 불린다.

- 행 교환(Row swapping): 행렬의 두 행을 서로 교환하여 계산을 쉽게 만듭니다. 아래 행렬을 보면 보기행렬의 1행과 3행을 교환한 것을 알 수 있습니다. 이를 수학식으로 표현하면 아래와 같습니다.

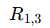
- 행 스칼라 곱(Row scaling): 행의 모든 요소에 같은 숫자를 곱하여 연산을 간편하게 합니다. 행렬에서 두번째행에 2를 곱하면 위와 같은 행렬을 얻을 수 있습니다. 이를 수학식으로 표현하면 다음과 같습니다.


- 행 더하기(Row addition): 한 행에 다른 행의 배수를 더하거나 빼서 특정 요소를 0으로 만듭니다. 보기행렬의 첫 번째 행에 두 번째 행의 2배를 빼면 다음과 같습니다. 복잡해보일 수 있으나 2행에 2를 곱한 값 8, 10, 12를 1행에 뺀 것이다. 이를 수학적으로 표현하면 아래와 같다.


이상으로 가우스소거법과 기본행연산에 대해서 포스팅하였습니다. 요즘 선형대수를 공부해서 복습삼아 포스팅해보았습니다. 궁금하신 점 있으시면 댓글로 남겨주시면 같이 공부되고 좋을 것 같습니다. 감사합니다.
반응형
'공부 > 컴퓨터' 카테고리의 다른 글
| 저급언어 VS 고급언어 (33) | 2024.09.20 |
|---|---|
| 다양한 프로그래밍 언어들(Python/Java/C++/JavaScript/C#/PHP) (47) | 2024.09.11 |
| 행렬이란? 행렬의 덧셈/뺄셈/곱셈/전치행렬/단위행렬/역행렬/행렬식 (18) | 2024.09.09 |
| 방정식(일차방정식/연립방정식/해의 종류/연립방정식푸는방법) (32) | 2024.09.07 |
| 스크래치란? 스크래치의 특징/장점/방법 (39) | 2024.09.05 |




